Chegg Again With GX Defined as Above Setting Þâ¼2 and Ïæ’24 Evaluate the Following

Show Mobile Find Bear witness All NotesHibernate All Notes

Mobile Observe

You announced to be on a device with a "narrow" screen width (i.e. yous are probably on a mobile telephone). Due to the nature of the mathematics on this site it is all-time views in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (should be able to whorl to see them) and some of the menu items will exist cut off due to the narrow screen width.

Section half dozen-iv : Surface Integrals of Vector Fields

But every bit nosotros did with line integrals nosotros now need to move on to surface integrals of vector fields. Recall that in line integrals the orientation of the curve nosotros were integrating along could change the answer. The same matter volition concord true with surface integrals. So, before we really go into doing surface integrals of vector fields we beginning need to introduce the idea of an oriented surface.

Let'south offset off with a surface that has ii sides (while this may seem strange, retrieve that the Mobius Strip is a surface that only has ane side!) that has a tangent aeroplane at every point (except possibly along the boundary). Making this supposition means that every point volition have ii unit of measurement normal vectors, \({\vec n_1}\) and \({\vec n_2} = - {\vec n_1}\). This means that every surface will accept two sets of normal vectors. The prepare that we choose will give the surface an orientation.

In that location is one convention that we will make in regard to certain kinds of oriented surfaces. First, we need to define a closed surface. A surface \(S\) is closed if it is the boundary of some solid region \(E\). A good instance of a closed surface is the surface of a sphere. We say that the closed surface \(S\) has a positive orientation if we cull the set of unit normal vectors that point outward from the region \(Due east\) while the negative orientation volition exist the set of unit normal vectors that bespeak in towards the region \(E\).

Notation that this convention is merely used for closed surfaces.

In society to piece of work with surface integrals of vector fields nosotros will demand to be able to write downwards a formula for the unit normal vector respective to the orientation that nosotros've chosen to work with. We take two ways of doing this depending on how the surface has been given to usa.

First, permit'south suppose that the function is given past \(z = g\left( {10,y} \right)\). In this case we offset define a new function,

\[f\left( {ten,y,z} \right) = z - 1000\left( {x,y} \right)\]

In terms of our new function the surface is then given by the equation \(f\left( {x,y,z} \correct) = 0\). Now, call up that \(\nabla f\) will be orthogonal (or normal) to the surface given past \(f\left( {10,y,z} \right) = 0\). This means that we have a normal vector to the surface. The just potential problem is that it might not be a unit of measurement normal vector. That isn't a problem since we also know that nosotros can turn any vector into a unit of measurement vector by dividing the vector by its length. In our instance this is,

\[\vec northward = \frac{{\nabla f}}{{\left\| {\nabla f} \right\|}}\]

In this case it will exist convenient to really compute the gradient vector and plug this into the formula for the normal vector. Doing this gives,

\[\vec n = \frac{{\nabla f}}{{\left\| {\nabla f} \right\|}} = \frac{{ - {g_x}\,\vec i - {g_y}\,\vec j + \vec k}}{{\sqrt {{{\left( {{g_x}} \right)}^2} + {{\left( {{g_y}} \right)}^ii} + 1} }}\]

At present, from a notational standpoint this might not have been and then convenient, but it does allow us to brand a couple of additional comments.

Kickoff, observe that the component of the normal vector in the \(z\)-management (identified past the \(\vec k\) in the normal vector) is always positive and so this normal vector will generally bespeak upwards. It may not bespeak directly upwardly, simply it will take an upward component to it.

This volition be important when we are working with a closed surface and we want the positive orientation. If we know that we can then look at the normal vector and make up one's mind if the "positive" orientation should point upwardly or downward. Recollect that the "positive" orientation must point out of the region and this may mean downwards in places. Of course, if it turns out that we need the downward orientation we can ever take the negative of this unit vector and we'll get the one that we need. Again, think that nosotros e'er have that choice when choosing the unit of measurement normal vector.

Before we move onto the 2nd method of giving the surface nosotros should signal out that we only did this for surfaces in the form \(z = g\left( {x,y} \right)\). We could simply as easily done the above piece of work for surfaces in the form \(y = g\left( {x,z} \right)\) (so \(f\left( {x,y,z} \right) = y - g\left( {x,z} \right)\)) or for surfaces in the form \(x = m\left( {y,z} \right)\) (so \(f\left( {x,y,z} \right) = 10 - g\left( {y,z} \correct)\)).

Now, we need to discuss how to find the unit normal vector if the surface is given parametrically as,

\[\vec r\left( {u,v} \right) = ten\left( {u,v} \right)\vec i + y\left( {u,5} \right)\vec j + z\left( {u,5} \right)\vec k\]

In this case recollect that the vector \({\vec r_u} \times {\vec r_v}\) will be normal to the tangent plane at a detail betoken. Merely if the vector is normal to the tangent plane at a point then information technology will as well exist normal to the surface at that indicate. So, this is a normal vector. In order to guarantee that it is a unit of measurement normal vector we will also demand to split up it by its magnitude.

And so, in the case of parametric surfaces one of the unit normal vectors will be,

\[\vec n = \frac{{{{\vec r}_u} \times {{\vec r}_v}}}{{\left\| {{{\vec r}_u} \times {{\vec r}_v}} \right\|}}\]

As with the start case nosotros will need to wait at this once it'due south computed and decide if information technology points in the correct direction or not. If it doesn't then we tin can ever accept the negative of this vector and that will point in the correct direction.

Finally, think that we can always parameterize whatsoever surface given past \(z = g\left( {x,y} \right)\) (or \(y = g\left( {x,z} \right)\) or \(ten = g\left( {y,z} \correct)\)) easily enough and so if nosotros want to we tin can always employ the parameterization formula to discover the unit normal vector.

Okay, now that we've looked at oriented surfaces and their associated unit of measurement normal vectors nosotros can actually requite a formula for evaluating surface integrals of vector fields.

Given a vector field \(\vec F\) with unit of measurement normal vector \(\vec northward\) then the surface integral of \(\vec F\) over the surface \(Southward\) is given past,

\[\iint\limits_{South}{{\vec F\centerdot d\vec S}} = \iint\limits_{Due south}{{\vec F\centerdot \vec n\,dS}}\]

where the right paw integral is a standard surface integral. This is sometimes called the flux of \(\vec F\) across \(Southward\).

Before nosotros piece of work any examples permit'southward discover that nosotros can substitute in for the unit normal vector to get a somewhat easier formula to employ. We volition demand to be careful with each of the post-obit formulas still as each will assume a certain orientation and we may take to change the normal vector to match the given orientation.

Let's first outset past assuming that the surface is given by \(z = g\left( {x,y} \right)\). In this case let's also assume that the vector field is given by \(\vec F = P\,\vec i + Q\,\vec j + R\,\vec one thousand\) and that the orientation that we are after is the "upwards" orientation. Under all of these assumptions the surface integral of \(\vec F\) over \(S\) is,

\[\begin{align*}\iint\limits_{Southward}{{\vec F\centerdot d\vec Southward}} & = \iint\limits_{S}{{\vec F\centerdot \vec n\,dS}}\\ & = \iint\limits_{D}{{\left( {P\,\vec i + Q\,\vec j + R\,\vec k} \right)\centerdot \left( {\frac{{ - {g_x}\,\vec i - {g_y}\,\vec j + \vec g}}{{\sqrt {{{\left( {{g_x}} \right)}^ii} + {{\left( {{g_y}} \right)}^2} + ane} }}} \correct)}}\sqrt {{{\left( {{g_x}} \right)}^2} + {{\left( {{g_y}} \right)}^2} + i} \,dA\\ & = \iint\limits_{D}{{\left( {P\,\vec i + Q\,\vec j + R\,\vec k} \right)\centerdot \left( { - {g_x}\,\vec i - {g_y}\,\vec j + \vec m} \right)}}\,dA\\ & = \iint\limits_{D}{{ - P{g_x} - Q{g_y} + R}}\,dA\end{align*}\]

Now, remember that this causeless the "upward" orientation. If we'd needed the "downward" orientation, and then we would need to alter the signs on the normal vector. This would in plow change the signs on the integrand likewise. So, we really demand to be conscientious hither when using this formula. In general, information technology is best to rederive this formula as you demand it.

When we've been given a surface that is non in parametric form there are in fact vi possible integrals hither. 2 for each form of the surface \(z = g\left( {x,y} \right)\), \(y = thousand\left( {10,z} \right)\) and \(x = g\left( {y,z} \right)\). Given each form of the surface there will be ii possible unit normal vectors and we'll demand to choose the correct ane to lucifer the given orientation of the surface. However, the derivation of each formula is similar to that given here then shouldn't be likewise bad to exercise equally you need to.

Notice as well that because we are using the unit normal vector the messy square root will ever driblet out. This means that when we practice need to derive the formula we won't actually demand to put this in. All we'll need to work with is the numerator of the unit of measurement vector. We will see at least 1 more of these derived in the examples beneath. It should too exist noted that the square root is zippo more than than,

\[\sqrt {{{\left( {{g_x}} \right)}^2} + {{\left( {{g_y}} \right)}^2} + one} = \left\| {\nabla f} \right\|\]

so in the following work we will probably just utilise this note in place of the foursquare root when nosotros can to brand things a little simpler.

Allow's at present take a quick await at the formula for the surface integral when the surface is given parametrically by \(\vec r\left( {u,v} \right)\). In this case the surface integral is,

\[\brainstorm{align*}\iint\limits_{Southward}{{\vec F\centerdot d\vec S}} & = \iint\limits_{South}{{\vec F\centerdot \vec n\,dS}}\\ & = \iint\limits_{D}{{\vec F\centerdot \left( {\frac{{{{\vec r}_u} \times {{\vec r}_v}}}{{\left\| {{{\vec r}_u} \times {{\vec r}_v}} \correct\|}}} \right)\left\| {{{\vec r}_u} \times {{\vec r}_v}} \correct\|\,dA}}\\ & = \iint\limits_{D}{{\vec F\centerdot \left( {{{\vec r}_u} \times {{\vec r}_v}} \right)\,dA}}\cease{marshal*}\]

Again, annotation that we may take to change the sign on \({\vec r_u} \times {\vec r_v}\) to lucifer the orientation of the surface and then at that place is in one case again really ii formulas here. Also notation that once again the magnitude cancels in this case and so we won't demand to worry that in these problems either.

Note also that there are even times when we will apply the definition, \(\iint\limits_{Due south}{{\vec F\centerdot d\vec S}} = \iint\limits_{Due south}{{\vec F\centerdot \vec n\,dS}}\), direct. We will see an example of this beneath.

Let's now piece of work a couple of examples.

Example 1 Evaluate \( \displaystyle \iint\limits_{Southward}{{\vec F\centerdot d\vec S}}\) where \(\vec F = y\,\vec j - z\,\vec chiliad\) and \(South\) is the surface given past the paraboloid \(y = {10^2} + {z^2}\), \(0 \le y \le 1\) and the disk \({x^2} + {z^2} \le 1\) at \(y = 1\). Presume that \(S\) has positive orientation.

Evidence Solution

Okay, first let'south notice that the disk is really nothing more than the cap on the paraboloid. This means that we have a closed surface. This is important because we've been told that the surface has a positive orientation and past convention this means that all the unit normal vectors will need to point outwards from the region enclosed by \(Southward\).

Let's first become a sketch of \(South\) so nosotros can get a feel for what is going on and in which direction we will need to unit normal vectors to signal.

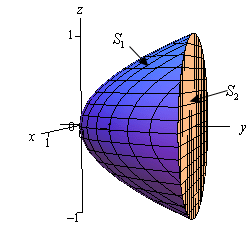
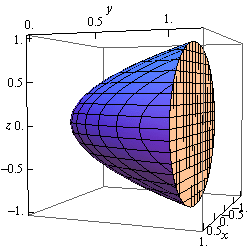
As noted in the sketch nosotros will denote the paraboloid by \({S_1}\) and the disk past \({S_2}\). As well note that in social club for unit normal vectors on the paraboloid to point away from the region they volition all demand to point generally in the negative \(y\) direction. On the other hand, unit normal vectors on the disk will demand to indicate in the positive \(y\) management in order to point away from the region.

Since \(South\) is composed of the two surfaces we'll demand to exercise the surface integral on each so add together the results to get the overall surface integral. Let's showtime with the paraboloid. In this case we have the surface in the class \(y = g\left( {x,z} \right)\) so we will demand to derive the right formula since the one given initially wasn't for this kind of function. This is easy plenty to do all the same. First define,

\[f\left( {ten,y,z} \right) = y - g\left( {ten,z} \correct) = y - {x^2} - {z^2}\]

We volition adjacent need the gradient vector of this part.

\[\nabla f = \left\langle { - 2x,1, - 2z} \right\rangle \]

At present, the \(y\) component of the gradient is positive and so this vector will generally indicate in the positive \(y\) direction. However, as noted above we need the normal vector betoken in the negative \(y\) direction to brand sure that information technology will be pointing abroad from the enclosed region. This means that we will need to use

\[\vec northward = \frac{{ - \nabla f}}{{\left\| { - \nabla f} \right\|}} = \frac{{\left\langle {2x, - ane,2z} \right\rangle }}{{\left\| {\nabla f} \right\|}}\]

Let'south notation a couple of things hither before we go on. We don't actually demand to divide this by the magnitude of the gradient since this will simply abolish out one time we actually do the integral. And so, because of this we didn't bother calculating it. Also, the dropping of the minus sign is not a typo. When we compute the magnitude we are going to foursquare each of the components and and so the minus sign will drop out.

\({S_1}\) : The Paraboloid

Okay, here is the surface integral in this case.

\[\begin{marshal*}\iint\limits_{{{S_1}}}{{\vec F\centerdot d\vec S}} & = \iint\limits_{D}{{\left( {y\,\vec j - z\,\vec g} \right)\centerdot \left( {\frac{{\left\langle {2x, - 1,2z} \right\rangle }}{{\left\| {\nabla f} \right\|}}} \right)\,\left\| {\nabla f} \correct\|\,dA}}\\ & = \iint\limits_{D}{{ - y - two{z^2}\,dA}}\\ & = \iint\limits_{D}{{ - \left( {{x^2} + {z^2}} \right) - 2{z^2}\,dA}}\\ & = - \iint\limits_{D}{{{x^2} + 3{z^2}\,dA}}\end{marshal*}\]

Don't forget that we need to plug in the equation of the surface for \(y\) before we actually compute the integral. In this case \(D\) is the disk of radius ane in the \(xz\)-plane and so it makes sense to use polar coordinates to complete this integral. Here are polar coordinates for this region.

\[\brainstorm{array}{c}x = r\cos \theta \hspace{0.5in}z = r\sin \theta \\ 0 \le \theta \le 2\pi \hspace{0.5in}0 \le r \le i\terminate{array}\]

Annotation that we kept the \(x\) conversion formula the same every bit the 1 nosotros are used to using for \(ten\) and let \(z\) be the formula that used the sine. We could have done information technology any order, nonetheless in this way we are at least working with ane of them every bit we are used to working with.

Hither is the evaluation of this integral.

\[\begin{align*}\iint\limits_{{{S_1}}}{{\vec F\centerdot d\vec S}} & = - \iint\limits_{D}{{{x^2} + three{z^2}\,dA}}\\ & = - \int_{{\,0}}^{{\,2\pi }}{{\int_{{\,0}}^{{\,1}}{{\left( {{r^two}{{\cos }^two}\theta + three{r^2}{{\sin }^ii}\theta } \right)r\,dr}}\,d\theta }}\\ & = - \int_{{\,0}}^{{\,two\pi }}{{\int_{{\,0}}^{{\,ane}}{{\left( {{{\cos }^ii}\theta + iii{{\sin }^2}\theta } \correct){r^3}\,dr}}\,d\theta }}\\ & = - \int_{{\,0}}^{{\,2\pi }}{{\left( {\frac{1}{2}\left( {1 + \cos \left( {2\theta } \right)} \correct) + \frac{three}{2}\left( {ane - \cos \left( {2\theta } \correct)} \correct)} \right)\left. {\left( {\frac{1}{4}{r^4}} \right)} \right|_0^1\,d\theta }}\\ & = - \frac{1}{8}\int_{{\,0}}^{{\,2\pi }}{{4 - 2\cos \left( {2\theta } \correct)\,d\theta }}\\ & = - \left. {\frac{ane}{viii}\left( {four\theta - \sin \left( {2\theta } \correct)} \right)} \correct|_0^{2\pi }\\ & = - \pi \end{align*}\]

\({S_2}\) : The Cap of the Paraboloid

We can now do the surface integral on the disk (cap on the paraboloid). This one is actually fairly easy to do and in fact we tin use the definition of the surface integral directly. First allow's notice that the disk is actually simply the portion of the plane \(y = i\) that is in front of the deejay of radius 1 in the \(xz\)-aeroplane.

At present we want the unit of measurement normal vector to bespeak away from the enclosed region and since it must besides be orthogonal to the plane \(y = 1\) then it must point in a management that is parallel to the \(y\)-centrality, simply we already accept a unit vector that does this. Namely,

\[\vec n = \vec j\]

the standard unit of measurement footing vector. It as well points in the correct management for u.s. to use. Because we have the vector field and the normal vector we can plug directly into the definition of the surface integral to get,

\[\iint\limits_{{{S_2}}}{{\vec F\centerdot d\vec Due south}} = \iint\limits_{{{S_2}}}{{\left( {y\,\vec j - z\,\vec thou} \right)\centerdot \left( {\vec j} \right)\,dS}}\, = \iint\limits_{{{S_2}}}{{y\,dS}}\]

At this point we demand to plug in for \(y\) (since \({S_2}\)is a portion of the plane \(y = 1\) we do know what it is) and we'll besides need the square root this time when we catechumen the surface integral over to a double integral. In this instance since we are using the definition straight we won't get the canceling of the square root that we saw with the first portion. To get the square root well need to acknowledge that

\[y = 1 = g\left( {x,z} \right)\]

and so the square root is,

\[\sqrt {{{\left( {{g_x}} \right)}^ii} + 1 + {{\left( {{g_z}} \correct)}^two}} \]

The surface integral is then,

\[\begin{marshal*}\iint\limits_{{{S_2}}}{{\vec F\centerdot d\vec S}} & = \iint\limits_{{{S_2}}}{{y\,dS}}\\ & = \iint\limits_{D}{{i\sqrt {0 + 1 + 0} \,dA}} = \iint\limits_{D}{{dA}}\end{align*}\]

At this point we can admit that \(D\) is a disk of radius 1 and this double integral is aught more the double integral that will give the area of the region \(D\) so in that location is no reason to compute the integral. Hither is the value of the surface integral.

\[\iint\limits_{{{S_2}}}{{\vec F\centerdot d\vec Southward}} = \pi \]

Finally, to finish this off we merely need to add the 2 parts upwards. Hither is the surface integral that we were actually asked to compute.

\[\iint\limits_{S}{{\vec F\centerdot d\vec Southward}} = \iint\limits_{{{S_1}}}{{\vec F\centerdot d\vec Southward}} + \iint\limits_{{{S_2}}}{{\vec F\centerdot d\vec Southward}} = - \pi + \pi = 0\]

Example two Evaluate \( \displaystyle \iint\limits_{S}{{\vec F\centerdot d\vec S}}\) where \(\vec F = ten\,\vec i + y\,\vec j + {z^iv}\,\vec grand\) and \(S\) is the upper half the sphere \({x^2} + {y^2} + {z^2} = 9\) and the deejay \({x^ii} + {y^2} \le ix\) in the plane \(z = 0\). Assume that \(S\) has the positive orientation.

Testify Solution

So, equally with the previous problem we have a closed surface and since we are also told that the surface has a positive orientation all the unit of measurement normal vectors must point away from the enclosed region. To aid united states visualize this here is a sketch of the surface.

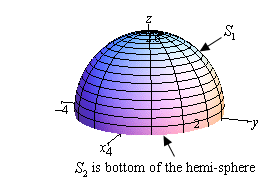
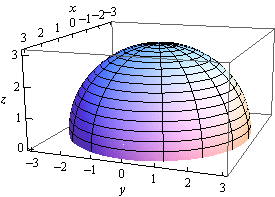
We will call \({S_1}\) the hemisphere and \({S_2}\) will be the bottom of the hemisphere (which isn't shown on the sketch). Now, in order for the unit normal vectors on the sphere to point away from enclosed region they volition all need to have a positive \(z\) component. Recollect that the vector must be normal to the surface and if there is a positive \(z\) component and the vector is normal it volition have to be pointing away from the enclosed region.

On the other hand, the unit normal on the lesser of the disk must point in the negative \(z\) direction in order to point away from the enclosed region.

\({S_1}\) : The Sphere

Let'southward do the surface integral on \({S_1}\) first. In this case since the surface is a sphere we volition need to utilise the parametric representation of the surface. This is,

\[\vec r\left( {\theta ,\varphi } \right) = iii\sin \varphi \cos \theta \,\vec i + 3\sin \varphi \sin \theta \,\vec j + iii\cos \varphi \,\vec k\]

Since we are working on the hemisphere here are the limits on the parameters that we'll need to employ.

\[0 \le \theta \le 2\pi \hspace{0.25in}\hspace{0.25in}0 \le \varphi \le \frac{\pi }{2}\]

Next, nosotros need to determine \({\vec r_\theta } \times {\vec r_\varphi }\). Here are the two individual vectors and the cross product.

\[\brainstorm{marshal*}{{\vec r}_\theta }\left( {\theta ,\varphi } \correct) & = - three\sin \varphi \sin \theta \,\vec i + 3\sin \varphi \cos \theta \,\vec j\\ {{\vec r}_\varphi }\left( {\theta ,\varphi } \right) & = 3\cos \varphi \cos \theta \,\vec i + 3\cos \varphi \sin \theta \,\vec j - three\sin \varphi \,\vec k\end{align*}\] \[\begin{align*}{{\vec r}_\theta } \times {{\vec r}_\varphi } & = \left| {\begin{assortment}{*{20}{c}}{\vec i}&{\vec j}&{\vec k}\\{ - 3\sin \varphi \sin \theta }&{3\sin \varphi \cos \theta }&0\\{iii\cos \varphi \cos \theta }&{3\cos \varphi \sin \theta }&{ - iii\sin \varphi }\terminate{array}} \right|\\ & = - 9{\sin ^two}\varphi \cos \theta \,\vec i - 9\sin \varphi \cos \varphi {\sin ^two}\theta \,\vec k - 9{\sin ^ii}\varphi \sin \theta \,\vec j - 9\sin \varphi \cos \varphi {\cos ^two}\theta \,\vec k\\ & = - 9{\sin ^ii}\varphi \cos \theta \,\vec i - 9{\sin ^2}\varphi \sin \theta \,\vec j - 9\sin \varphi \cos \varphi \left( {{{\sin }^two}\theta \, + {{\cos }^2}\theta } \correct)\vec k\\ & = - 9{\sin ^2}\varphi \cos \theta \,\vec i - nine{\sin ^ii}\varphi \sin \theta \,\vec j - ix\sin \varphi \cos \varphi \,\vec k\finish{marshal*}\]

Notation that we won't need the magnitude of the cross product since that will abolish out once we start doing the integral.

Notice that for the range of \(\varphi \) that we've got both sine and cosine are positive and and so this vector will accept a negative \(z\) component and as nosotros noted higher up in order for this to point away from the enclosed area we will need the \(z\) component to be positive. Therefore, we volition demand to use the following vector for the unit normal vector.

\[\vec n = - \frac{{{{\vec r}_\theta } \times {{\vec r}_\varphi }}}{{\left\| {{{\vec r}_\theta } \times {{\vec r}_\varphi }} \right\|}} = \frac{{9{{\sin }^2}\varphi \cos \theta \,\vec i + 9{{\sin }^2}\varphi \sin \theta \,\vec j + 9\sin \varphi \cos \varphi \,\vec k}}{{\left\| {{{\vec r}_\theta } \times {{\vec r}_\varphi }} \right\|}}\]

Again, we will drop the magnitude once we get to actually doing the integral since it will just cancel in the integral.

Okay, next we'll need

\[\vec F\left( {\vec r\left( {\theta ,\varphi } \correct)} \correct) = 3\sin \varphi \cos \theta \,\vec i + 3\sin \varphi \sin \theta \,\vec j + 81{\cos ^4}\varphi \,\vec k\]

Remember that in this evaluation we are merely plugging in the \(x\) component of \(\vec r\left( {\theta ,\varphi } \right)\) into the vector field etc.

We also may as well get the dot product out of the style that we know we are going to need.

\[\begin{align*}\vec F\left( {\vec r\left( {\theta ,\varphi } \correct)} \correct)\centerdot \left(- {{{\vec r}_\theta } \times {{\vec r}_\varphi }} \right) & = 27{\sin ^3}\varphi {\cos ^2}\theta + 27{\sin ^three}\varphi {\sin ^ii}\theta + 729\sin \varphi {\cos ^5}\varphi \\ & = 27{\sin ^3}\varphi + 729\sin \varphi {\cos ^5}\varphi \end{align*}\]

At present we can practise the integral.

\[\begin{align*}\iint\limits_{{{S_{\,i}}}}{{\vec F\centerdot d\vec S}} & = \iint\limits_{D}{{\vec F\centerdot \left( {\frac{{{{\vec r}_\theta} \times {{\vec r}_\varphi}}}{{\left\| {{{\vec r}_\theta } \times {{\vec r}_\varphi }} \right\|}}} \correct)\,\left\| {{{\vec r}_\theta } \times {{\vec r}_\varphi }} \right\|\,\,dA}}\\ & = \int_{{\,0}}^{{\,2\pi }}{{\int_{{\,0}}^{{\frac{\pi }{2}}}{{27{{\sin }^3}\varphi + 729\sin \varphi {{\cos }^5}\varphi \,d\varphi }}\,d\theta }}\\ & = \int_{{\,0}}^{{\,2\pi }}{{\int_{{\,0}}^{{\frac{\pi }{2}}}{{27\sin \varphi \left( {ane - {{\cos }^2}\varphi } \correct) + 729\sin \varphi {{\cos }^5}\varphi \,d\varphi }}\,d\theta }}\\ & = - \int_{{\,0}}^{{\,two\pi }}{{\left. {\left( {27\left( {\cos \varphi - \frac{1}{3}{{\cos }^3}\varphi } \right) + \frac{{729}}{vi}{{\cos }^vi}\varphi } \right)} \right|_0^{\frac{\pi }{2}}\,d\theta }}\\ & = \int_{{\,0}}^{{\,2\pi }}{{\frac{{279}}{2}\,d\theta }}\\ & = 279\pi \stop{align*}\]

\({S_2}\) : The Bottom of the Hemi-Sphere

Now, we need to do the integral over the lesser of the hemisphere. In this case nosotros are looking at the disk \({x^two} + {y^2} \le nine\) that lies in the plane \(z = 0\) and then the equation of this surface is actually \(z = 0\). The deejay is really the region \(D\) that tells us how much of the surface we are going to use. This also means that we tin can use the definition of the surface integral here with

\[\vec n = - \vec k\]

We need the negative since it must point away from the enclosed region.

The surface integral in this case is,

\[\begin{align*}\iint\limits_{{{S_2}}}{{\vec F\centerdot d\vec Southward}} & = \iint\limits_{{{S_2}}}{{\left( {x\,\vec i + y\,\vec j + {z^four}\,\vec k} \right)\centerdot \left( { - \vec thou} \correct)\,dS}}\,\\ & = \iint\limits_{{{S_2}}}{{ - {z^4}\,dS}}\end{align*}\]

Remember, nonetheless, that we are in the plane given past \(z = 0\) and so the surface integral becomes,

\[\iint\limits_{{{S_2}}}{{\vec F\centerdot d\vec South}} = \iint\limits_{{{S_2}}}{{ - {z^4}\,dS}} = \iint\limits_{{{S_2}}}{{0\,dS}} = 0\]

The last step is to and so add the two pieces up. Hither is surface integral that nosotros were asked to look at.

\[\iint\limits_{S}{{\vec F\centerdot d\vec South}} = \iint\limits_{{{S_1}}}{{\vec F\centerdot d\vec Southward}} + \iint\limits_{{{S_2}}}{{\vec F\centerdot d\vec South}} = 279\pi + 0 = 279\pi \]

Nosotros will leave this department with a quick interpretation of a surface integral over a vector field. If \(\vec v\) is the velocity field of a fluid then the surface integral

\[\iint\limits_{S}{{\vec v\centerdot d\vec S}}\]

represents the book of fluid flowing through \(S\) per time unit (i.east. per second, per minute, or whatever time unit of measurement you are using).

vumonesty.blogspot.com

Source: https://tutorial.math.lamar.edu/classes/calcIII/SurfIntVectorField.aspx

Share this post